零知识证明入门

无论是在聊 L2、隐私还是下一代 Web 技术，零知识证明都是经常会碰到的技术术语，听起来就像是科幻小说里的东西：向你证明我知道一个秘密，但绝不透露这个秘密本身，这简直是程序员的终极浪漫。

大多数人粗看都会觉得这东西是密码学博士们的专属玩具，我花了一段时间学习后，发现这条通往魔法世界的路似乎有迹可循，希望这篇入门介绍能帮助到更多这方向的学习者。

魔法洞穴

忘掉所有数学，我们先从一个故事开始——“阿里巴巴洞穴”，这是理解 ZKP 最经典的例子，最早由 Jean-Jacques Quisquater 等人于 1990 年在他们的论文《如何向你的孩子解释零知识协议》中发表。

想象一个环形洞穴，A、B 两个入口在前方，深处有一扇只有知道咒语才能打开的魔法门。Alice 知道咒语，现在，Alice 想向 Bob 证明她知道咒语，但又不想让 Bob 听到咒语是什么。

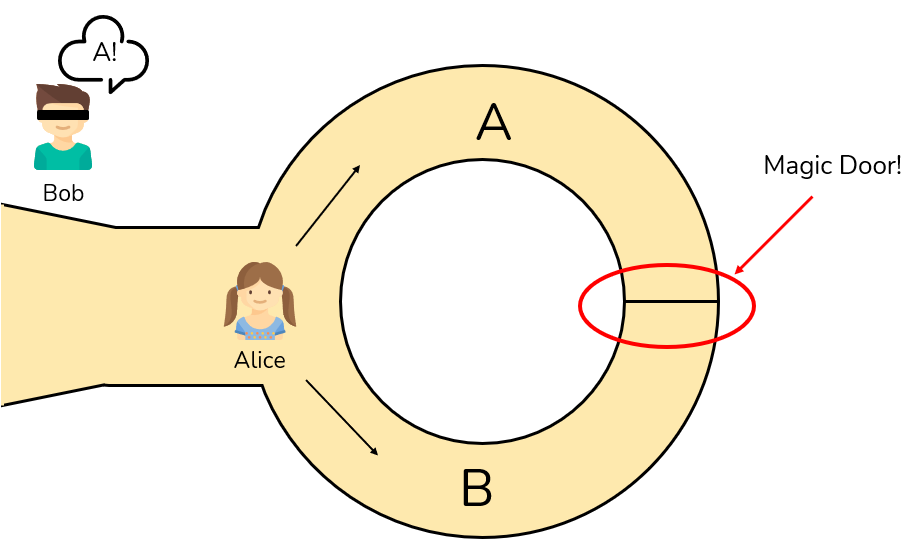
他们可以这样玩一个游戏：

承诺 (Commitment)：Alice，作为证明者 (Prover)，独自进入洞穴。然后可以随机从 A 口进，也可以从 B 口进。Bob 在洞外等着，但不知道 Alice 走了哪条路。
挑战 (Challenge)：Bob 作为验证者 (Verifier)，走到洞口然后随机喊出一个要求，比如：“从 B 通道出来！”
响应 (Response)：Alice 听到要求后：
- 如果她当初就是从 B 进去的，那简单，就直接从 B 走出来。
- 如果她当初是从 A 进去的，就必须念动咒语打开那扇魔法门穿过去，然后从 B 通道出来。
验证 (Verification)：Bob 看到 Alice 确实从 B 通道出来了，他对 Alice 的信任度增加了一点。

为什么说“一点”呢？因为如果 Alice 不知道咒语，她仍然有 50% 的概率蒙对（比如 Alice 从 B 进去，Bob 恰好也喊了 B）。

但如果这个游戏重复 20 次，Alice 每次都能从 Bob 指定的出口出来，那 Alice 每次都蒙对的概率就只有$$\left(\frac{1}{2}\right)^{20}$$，也就是大约是百万分之一。这时候 Bob 就有十足的把握相信，Alice 确实知道那个咒语。

这个小游戏完美地展示了 ZKP 的三大特性：

完整性 (Completeness)：如果 Alice 真的知道咒语，她总能完成挑战。
可靠性 (Soundness)：如果 Alice 不知道咒语，她几乎不可能骗过 Bob。
零知识性 (Zero-Knowledge)：在整个过程中，Bob 除了“Alice 知道咒语”这个事实外，没有学到任何关于咒语本身的信息。

另外我们可以看到一个重要的属性是，零知识证明并非数学意义上的证明，因为可能存在一个很小很小的概率，即可靠性误差 – 作弊的证明者能够骗过验证者，但实际实践中我们几乎可以忽略这个极小的概率。

Where’s Wally

还有另外一个比较简单的例子来说明零知识证明：

Alice 和 Bob 玩游戏看谁先找到 Wally，Alice 说她找到了，她想要证明自己已经得到了结果，但又不想透露更多信息给 Bob，所以她可以用一个几倍面积黑色的纸片遮住整个图画，然后把 Wally 位置那里在黑色纸片上打个小孔，这样 Bob 就可以看到 Wally，而不知道 Wally 在哪儿。注意这里为什么强调几倍面积的黑色纸片，如果是和原图相同大小的纸片，就可能暴露了 Wally 的大致方向和范围。

这个例子展示的 ZKP 另外一个特性是 Prover 通常是更耗费资源的 (从图片中找到 Wally 需要花费一定的时间)，而 Verifier 通常能很快验证。这个特性才能让一些区块链项目利用 ZKP 把链上计算挪到链下计算，而链上只是做验证。

最简单的 ZKP 代码

两个例子很棒，但代码怎么写？

我接触到的第一个协议叫 Schnorr 身份验证，它要证明的是：“我知道与公钥 h 对应的私钥 x，其中 h = g^x mod p”。这里的“咒语”就是 x，而那扇“魔法门”就是离散对数问题——从 g, h, p 反推出 x 极其困难。

这个协议的“交互式”版本，完美地复刻了洞穴里的“一来一回”：

Prover (我): 随机选个数 k，计算 t = g^k mod p 发给 Verifier。这叫“承诺”。
Verifier (你): 随机给 Prover 一个数 c，这叫“挑战”。
Prover: 根据收到的 c，计算 r = k - c*x mod (p-1) 并发回。这叫“响应”。
Verifier: 验证 g^r * h^c mod p 是不是等于 Prover 一开始给的 t。

完整代码在iteractive_schnorr

fn iteractive_schnorr() {
    // 公开参数：素数 p=204859, g=5, x=6 (秘密), h = 5^6 mod 204859 = 15625
    let p: BigInt = BigInt::from(204859u64);
    let g: BigInt = BigInt::from(5u32);
    let x: BigInt = BigInt::from(6u32); // 证明者的秘密
    let h = g.modpow(&x, &p); // h = g^x mod p

    // 进行多轮证明 p
    for _ in 0..20 {
        // 证明者：生成承诺 t = g^k mod p
        let mut rng = thread_rng();
        let k = rng.gen_bigint_range(&BigInt::one(), &(&p - BigInt::one()));
        let t = g.modpow(&k, &p);
        println!("证明者发送 t: {}", t);

        // 验证者：生成挑战 c (简化到 0..10)
        let c: BigInt = BigInt::from(rng.gen_range(0..10));
        println!("验证者挑战 c: {}", c);

        // 证明者：响应 r = k - c * x mod (p-1)
        let order = &p - BigInt::one(); // 阶
        let r = (&k - &c * &x).modpow(&BigInt::one(), &order); // 确保正数
        println!("证明者响应 r: {}", r);

        // 验证者：检查 g^r * h^c == t mod p
        let left = g.modpow(&r, &p) * h.modpow(&c, &p) % &p;
        if left == t {
            println!("验证通过！");
        } else {
            println!("验证失败！");
        }
    }
}

但一来一回也太麻烦了，互联网应用需要的是一次性的“证明”。经过一番研究，密码学家们想出的一个绝妙技巧，叫做 Fiat-Shamir 启发式证明。

它的核心思想是：用哈希函数来模拟一个不可预测的“挑战者”。

Prover 不再等待 Verifier 给出挑战 c，而是自己计算 c = hash(公开信息, 自己的承诺 t)。因为哈希函数的雪崩效应，Prover 无法预测 c 的值来作弊，这就巧妙地把交互过程压缩了。

我们可以用 Rust 写出这样一个完整的非交互式证明程序 fiat_shamir：

fn fiat_shamir() {
    // --- 公开参数 ---
    // 在真实世界，p 应该是至少 2048 位的安全素数
    let p: BigInt = BigInt::from(204859u64);
    let g: BigInt = BigInt::from(2u64);

    // Prover 的秘密 (只有 Prover 知道)
    let secret_x: BigInt = BigInt::from(123456u64);

    // Prover 的公钥 (所有人都知道)
    let public_h = g.modpow(&secret_x, &p);

    println!("--- 公开参数 ---");
    println!("p = {}", p);
    println!("g = {}", g);
    println!("h = g^x mod p = {}", public_h);
    println!("-------------------");

    // --- PROVER: 生成证明 ---
    println!("Prover 正在生成证明...");
    let mut rng = thread_rng();
    let order = &p - BigInt::one();

    // 1. 承诺：随机选一个 k, 计算 t = g^k mod p
    let k = rng.gen_bigint_range(&BigInt::one(), &order);
    let t = g.modpow(&k, &p);

    // 2. 挑战 (Fiat-Shamir 的魔法在这里!):
    // 把公开信息和承诺 t 一起哈希，模拟一个无法预测的挑战 c
    let mut hasher = Sha256::new();
    hasher.write_all(&g.to_bytes_be().1).unwrap();
    hasher.write_all(&public_h.to_bytes_be().1).unwrap();
    hasher.write_all(&t.to_bytes_be().1).unwrap();
    let hash_bytes = hasher.finalize();
    let c = BigInt::from_bytes_be(num_bigint::Sign::Plus, &hash_bytes) % &order;

    // 3. 响应：计算 r = k - c*x (mod order)
    let cx = (&c * &secret_x) % &order;
    let mut r = (&k - cx) % &order;
    if r < BigInt::zero() {
        r += &order;
    }

    println!("证明已生成：(r = {}, c = {})", r, c);
    println!("-------------------");

    // --- VERIFIER: 验证证明 ---
    println!("Verifier 正在验证证明...");
    // Verifier 为了验证，需要自己重新计算 t' = g^r * h^c mod p
    let gr = g.modpow(&r, &p);
    let hc = public_h.modpow(&c, &p);
    let t_prime = (&gr * &hc) % &p;

    // Verifier 再用算出来的 t' 计算 c' = H(g || h || t')
    let mut hasher = Sha256::new();
    hasher.write_all(&g.to_bytes_be().1).unwrap();
    hasher.write_all(&public_h.to_bytes_be().1).unwrap();
    hasher.write_all(&t_prime.to_bytes_be().1).unwrap();
    let hash_bytes = hasher.finalize();
    let c_prime = BigInt::from_bytes_be(num_bigint::Sign::Plus, &hash_bytes) % &order;

    if c == c_prime {
        println!("✅ 验证通过！");
    } else {
        println!("❌ 验证失败！");
    }
}

以上我们通过最简单的代码来演示了 ZKP 的基本思想，从数学原理上都是基于离散对数困难性。

发散到 Passkeys

当我看到 Hash 的时候，我联想到了后台服务的密码存储，比如我们在做一个用户注册和登录功能的时候，为了安全我们是不会去存储用户的原始密码（秘密），而是会使用密码哈希方案，去存储 hash(password + salt)。

但这个密码哈希方案其实也泄露了“知识”，当你登录时会把 123456 发送给服务器，服务器计算 hash("123456" + salt) 并与数据库中的值对比。

在传输过程中：密码是明文的（当然可以用 TLS/SSL 加密，但服务器在解密后会看到明文）。
对服务器而言：服务器在验证那一瞬间是知道你的密码的。
如果数据库被盗：攻击者拿到了 hash(password + salt) 的列表。这个哈希值本身就是一条重要的知识！它虽然不是密码原文，但它是密码的一个确定性指纹。攻击者可以进行：
- 字典攻击：尝试常用密码，计算哈希值来一一比对。
- 彩虹表攻击：用一个预先计算好的哈希值数据库来反查。
- 暴力破解：对所有可能的组合进行哈希计算。

这就是为什么我们需要“加盐（salt）”和使用慢哈希函数（如 Argon2, bcrypt），目的就是为了增加攻击者进行上述离线攻击的成本，但无论如何，哈希值本身就是泄露的“知识”。

所以如果我们要更安全，一点“知识”都不泄露，似乎 ZKP 适合做认证服务？注册时不存密码哈希，只存公钥 h。登录时，我发送一个 ZKP 证明，服务器验证一下就行了，数据库被拖库了都没事。

甚至更简单点其实就用公私钥对不是更方便和安全么，Nostr 就是这么做的 (钱包也是这个原理)，private key 是密码，每次发内容就用私钥签名内容，然后把 pubkey 带上，这样任何收到这条消息的节点都可以验证签名是否一致，这样就本质上通过各个 relay 节点形成一个去中心化的社交网络。

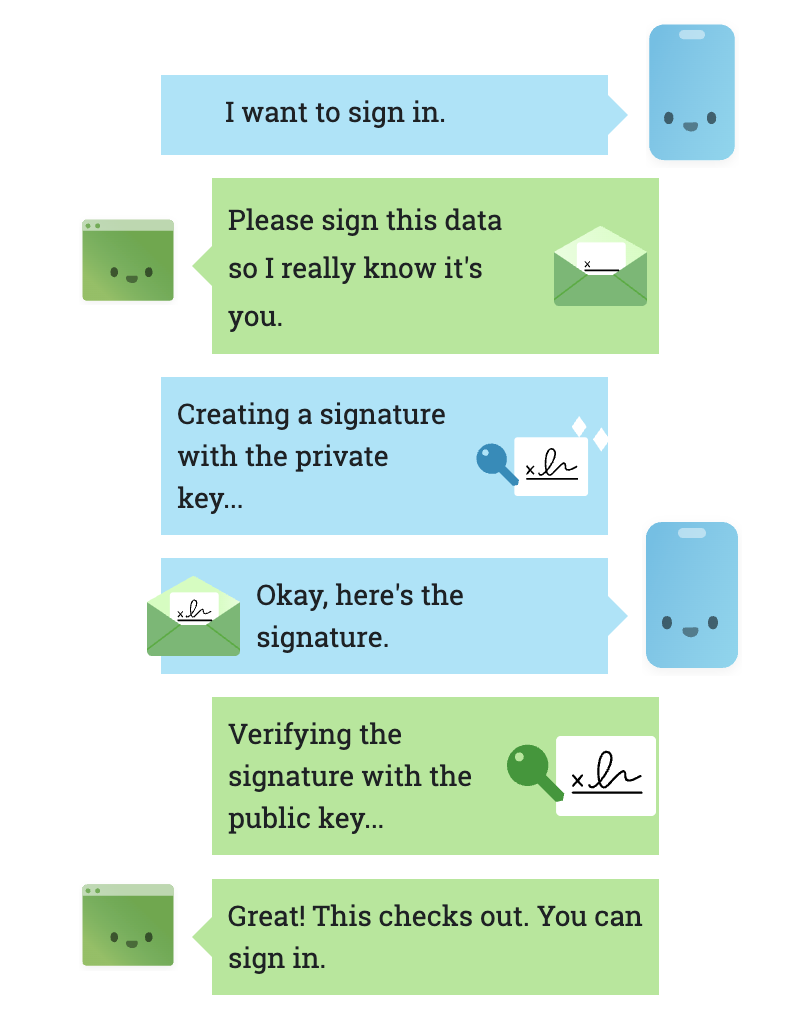
我按照这个思路去找 Web 相关的解决方案，业界给出的答案是 Passkeys (基于 WebAuthn 标准)，使用非对称加密来替代密码（私钥不出设备），Passkeys 是这样工作的：

注册： 你的设备（如 iPhone 或 Android 手机）在本地生成一对密钥（私钥和公钥）。私钥安全地存储在设备的硬件安全芯片中，永远不会离开设备。你把公钥发送给网站服务器。
登录：
- 网站向你的设备发送一个“挑战”（一个随机数）。
- 你的设备用私钥对这个“挑战”进行签名，然后把签名发回给网站。
- 网站用它存储的你的公钥来验证这个签名是否有效。
用户体验： 整个过程对于用户来说，可能只是做一次指纹识别或面部识别来授权设备使用私钥。

2019 年 3 月 4 日 WebAuthn Level 1 已经被 W3C 正式发布为“推荐标准 (Recommendation)”，标志着它成为了一个成熟、稳定、官方推荐的 Web 标准。

通过“电路”证明程序的运行

从上面的例子我们看到，ZKP 很适合用来证明 Prover 知道某个秘密，比如一个数 x ，但 ZKP 的用途远不止于此，还可以证明任何计算过程的正确性。

为什么证明一个程序正确运行很重要，因为像以太坊这样的公链，如果所有的节点都运行同样的合约 (本质上就是一段程序代码) 多次，这无疑是很大的浪费，我们想通过 ZKP 把计算挪到链下，这样公链上的节点只需要验证程序被正确执行就可。

“我正确运行了一个复杂的程序，得到了这个输出。”—— 这要怎么证明？

答案是四个字：万物皆可电路 (Arithmetization)。

ZKP 系统（比如我们后面会聊的 zk-SNARKs）的“世界观”非常单纯，甚至有点笨拙，它看不懂我们人类写的高级代码，比如 if/else 语句、for 循环。

如果我们想让 ZKP 为我们工作，就必须先把我们要证明的东西，翻译成它唯一能听懂的语言。这个翻译过程，就是“算术化 (Arithmetization)”。而“电路”或“约束系统”，就是我们翻译出来的最终稿。这个重写的过程，就是“拍扁 (Flattening)”。你把一个有层次、有复杂逻辑的程序，变成了一个长长的、线性的、只包含最基本算术运算的指令列表。

任何程序，无论多复杂，都可以被“拍扁”成一系列最基础的加法和乘法约束。比如 out = x*x*x + x + 5 这段代码，可以被分解为：

v1 = x * x
v2 = v1 * x
v3 = v2 + x
out = v3 + 5

于是，证明“我正确运行了程序”，就转化为了证明“我知道一组数 (x, v1, v2, v3, out) 能同时满足上面这一堆等式”。这个过程，就是把代码逻辑“算术化”，变成了 ZKP 系统可以处理的语言。

那我们来看 Verifier 如何验证上面的计算过程，最原始的当然是根据输入，来一条一条的执行上面被拍平后的指令集，但这样的工作量和自己去执行整个程序就差不多了。

为了避免这种蛮力验证，密码学家们引入了一个极其强大的数学工具：多项式 (Polynomials)。
整个魔法流程如下：

Prover 的艰巨任务：将所有约束“编织”进一个多项式 Prover 会执行一个惊人的转换：他会找到一种方法 (Groth16、PLONK、STARKs 等)，将我们前面提到的那一整个约束系统 (x * x - v1 = 0, v1 * x - v2 = 0, …) 全部编码成一个单一的、巨大的多项式方程。

我们可以把这个巨大的“主多项式”记为 P(z)。这个 P(z) 有一个神奇的特性：

当且仅当 Prover 提供的所有见证值 (x, v1, v2…) 都完全正确、满足所有原始约束时，这个主多项式 P(z) 在某些特定的点上才会等于 0。

如果 Prover 在任何地方作弊，哪怕只修改了一个微不足道的值，最终生成的那个 P(z) 就会是一个完全不同的多项式。
验证者的捷径 – 随机点检查 (Random Spot-Check) ：现在验证者的问题从“检查成千上万个小等式”变成了“如何验证 Prover 的那个巨大多项式 P(z) 是正确的？”

难道要把整个巨大的多项式传输过来再计算一遍吗？当然不是！这里用到了密码学中一个非常深刻的原理，通常与 Schwartz-Zippel 引理 有关。

它的直观思想是：

如果我有两个不同的、阶数很高的多项式 P(z) 和 F(z)（F 代表伪造的），然后我从一个极大的数域里随机挑选一个点 s，那么 P(s) 和 F(s) 的计算结果相等的概率几乎为零。

这就给了验证者一个巨大的捷径：
- Verifier 不需要关心那个巨大的多项式长什么样。
- 它只需要在一个秘密的、随机选择的点 s 上，对 Prover 的多项式进行一次“抽查”。
- 它通过密码学协议向 Prover 发起一个挑战：“嘿，你声称你有一个正确的多项式，那你告诉我，在 s 这个点上，你的多项式计算出来的值是多少？”

所以这里的 ZKP 证明里到底包含什么？

在一个典型的 zk-SNARK（比如 Groth16）中，那个小小的证明通常是由几个椭圆曲线上的点 (points on an elliptic curve) 组成的。可以把这些“点”想象成一种具备神奇数学特性的高级指纹。这些点就是 Prover 对他构造的那些巨大多项式（比如 A(x), B(x), C(x)，它们共同构成了我们之前说的那个主多项式 P(x)) 的“承诺”。

这里的魔法在于 Verifier 不需要通过这些“点”来反推出原始的多项式。相反，他可以直接在这些“点”上进行一种特殊运算，这种运算的结果等价于在原始多项式上进行“随机点检查”。这个特殊的运算，就是 zk-SNARKs 的核心引擎之一：配对 (Pairings)。并非所有 ZK 架构都用配对；Groth16/部分 KZG-based 系统用配对，STARKs 则用哈希/FRI 等替代方案。

让我们把整个流程串起来 (zk-SNARK)，看看 Prover 的多项式是如何被“隔空”验证的：

准备阶段 (Setup)：
- 协议约定好了一套公共参数（包含一个“验证密钥”）。这个验证密钥里编码了“游戏规则”，包括对程序正确性的期望。
Prover 的工作：
- 他有他的秘密“见证 (Witness)”。
- 他按照约定，将程序的约束系统转化成几个巨大的多项式 A(x), B(x), C(x)。（这些多项式满足 A(x) * B(x) - C(x) = H(x) * Z(x) 的关系，这是 R1CS 算术化的结果）。
- 关键一步：他并没有把这些多项式发出去。而是用他的“证明密钥”，计算出这几个多项式在某个秘密点 s 上的椭圆曲线点表示。这些点就是对多项式的“承诺”。
- 最终生成的证明 (Proof)，就是由这几个计算出来的椭圆曲线点组成的，它非常小。
Verifier 的工作：
- Verifier 收到这个由几个点组成的、小小的证明。
- Verifier 完全看不到 Prover 的任何多项式 (A(x), B(x), C(x))。
- Verifier 拿出“验证密钥”，并将 Prover 提交的这几个“承诺点”代入一个预设的配对验证方程 (Pairing Verification Equation)。
  
  这个方程被设计得极其巧妙，它的等号左边和右边分别对应着 Prover 原始多项式关系 A*B-C=H*Z 的加密形式。
  
  当且仅当 Prover 原始的、未知的那些多项式确实满足正确的数学关系时，这个配对验证方程的等号才能成立。

所以：

证明里是什么？ 是对 Prover 秘密多项式的密码学承诺（通常是几个椭圆曲线点）。
Verifier 如何知道多项式？ 他不需要知道。他只需要知道验证规则（即那个配对验证方程）。
如何验证？ 他把 Prover 的“承诺”（证明）代入“规则”（验证方程）。如果方程成立，他就知道那些他看不见的、被承诺了的多项式一定是正确的，进而推断出 Prover 的原始计算是正确的。

Prover 把“我知道所有题的答案”这个事实，通过复杂的计算，浓缩成了一个包含几个关键“密码学指纹”的信封（证明）。Verifier 不用拆开信封看所有答案，他只需要用一种特殊的“X 光机”（配对验证）照一下这个信封，就能瞬间知道里面的答案是不是都对。

ZKP 相关的应用

区块链因为其去中心化和对隐私性的严苛要求，ZKP 非常适合用在这个领域。

扩容 (ZK-Rollups): 让以太坊快如闪电

以太坊慢又贵，因为每个节点都要重复执行每笔交易。ZK-Rollup 的思路就像是找了个超级课代表：

在链下 (L2) 执行成千上万笔交易。
为“我已正确处理了这一切”这个声明，生成一个微小的 ZK 证明。
把这个证明提交到链上 (L1)。

L1 的所有节点不再需要重复计算那几千笔交易，它们只需要做一件极其廉价的事：验证那个 ZK 证明。就像老师检查作业，不再需要自己从头算一遍，只需要看一眼课代表盖的“全对”印章。

总而言之，Rollup 的核心创新在于将计算执行与数据结算分离。它利用 ZKP 等密码学技术，将繁重的“执行”环节放在链下，然后只把一个轻量的“证明”和必要数据放在链上进行“结算”，从而实现了对以太坊主网的大规模扩容。

隐私 (Tornado Cash): 你的钱，只有你知道

Tornado Cash 是个混币器，你存入 100 ETH，然后从一个全新的地址取出来，没人能把这两者联系起来。它的机制是：

存款：你在本地生成一个秘密凭证（包含Secret和Nullifier），然后计算出它的哈希值——“承诺 (Commitment)”，把承诺和钱一起存入合约。
取款：你用一个全新的地址，提交一个 ZK 证明，这个证明：“我知道某个树叶的 Secret 且未被花费”，同时提交 nullifier（通常是对秘密做散列得到的唯一标识）以标记已花费。这样合约无需关联存款者身份即可阻止双花。

整个过程，合约就像个盲人会计，它不知道是“谁”存的，也不知道取款对应的是“哪一一笔”存款，它只负责验证 ZKP 规则是否被遵守。

ZKP 在 AI 的应用

ZKP 应用在大模型也是最前沿、激动人心的领域。例如 AI 模型（尤其是大型语言模型）的权重是极其宝贵的商业机密。用户的数据又极其隐私。如何让一个 AI 模型在不暴露其内部权重的情况下，处理用户的隐私数据，并向用户证明它确实是用了那个宣称的高级模型，而不是一个廉价的“冒牌货”？

ZKP 解决方案 (ZKML - Zero-Knowledge Machine Learning)：
模型推理证明：模型提供方可以对一次推理过程生成 ZK 证明，证实“我使用我宣称的那个模型（其哈希值是公开的），处理了你的输入数据，得出了这个输出结果”。这向用户保证了模型的真实性，同时保护了模型的知识产权。

数据隐私证明：用户可以对自己的数据生成 ZK 证明，证实“我的数据（例如医疗记录）符合某个特定标准（例如，有某种疾病特征）”，然后将这个证明提交给 AI 模型进行统计或研究，而无需上传原始的隐私数据。

这里有更多相关的资料：An introduction to zero-knowledge machine learning (ZKML)

零知识证明和硬件

前面我们谈到，在 ZKP 中Prover（证明者）端计算量最大，主要集中在以下几个方面：

多项式承诺方案：这是现代零知识证明（如 zk-SNARKs、zk-STARKs）的核心。证明者需要将计算任务转化为多项式，并对这些多项式进行一系列复杂的加密运算，例如多项式插值、求导、卷积、快速傅里叶变换（FFT） 等。这些运算的复杂度很高，尤其是当要证明的计算规模很大时。
同态加密运算或椭圆曲线点运算：在一些零知识证明协议中，为了生成和验证证明，需要进行大量的椭圆曲线点乘运算。这种运算在数学上非常耗时，尤其是当需要处理大量的点时。
哈希函数计算：为了将复杂的数据结构或计算结果进行压缩和承诺，证明者会使用到大量的加密哈希函数，例如 SHA-256、Poseidon 等。

而在Verifier（验证者）端计算量相对较小，这也是零知识证明的重要优势之一，但它仍然需要进行一些关键的计算，比如：

椭圆曲线配对运算（Pairing）：在 zk-SNARKs 等协议中，验证者需要进行椭圆曲线配对运算来验证证明。这是一种特殊的加密操作，虽然比证明者的计算量小得多，但仍然需要一定的计算资源。
哈希函数和多项式求值：验证者也需要进行一些哈希计算和多项式求值来检查证明的有效性。

总的来说，零知识证明的计算量主要耗费在Prover端，因为它需要对整个计算过程进行完整的加密转换和证明生成，而这些步骤依赖于高复杂度的多项式和椭圆曲线运算。所以我们看到一些专门为此服务的硬件 FPGA、ASIC、GPU。

而 RISC-V 因为其可扩展性和模块化设计、开源的标准等优势，是实现零知识证明硬件加速的重要“基石”之一，risc0 是个值得关注的项目