那天师兄给面试，面到一道图算法题目，求图中两个点的前 K 短路径。当时觉得用 Dijkstra+heap 应该可以，不过也没想清楚。以前看到过这个，那时还没怎么仔细看图算法所以丢一边了，今天好好看了一下。简单一点的解法是用 Dijkstra+Astar。典型的题目就是POJ 2449。

A* 算法

再谈 A算法。A算法中的评估函数为 f(N)=cost(N)+h(N)。其中 cost(N) 为从源点到 N 点的距离，h(N) 为 N 点到终点的的一个评估路径长度，设 h(N) 为实际 N 点到终点的路径长度。只要满足条件：h(N)<=h(N)，那么用这个评估函数找到最短路径。具体证明看这篇论文A Formal Basis for the Heuristic Determination of Minimum Cost Paths。其优势在于在选择每个路径 上的点的时候给予了 h(N) 这个启发，在搜索空间中尽量选择可能最有可能产生最优解的下一个状态，使得搜索的时间都相应地减少。A算法的思想也是贪心 的，Dijkstra 是 A的一个特例，当 h(N)=0 时，A*就退化成了 Dijkstra 算法，那么就是盲目的扩展当前最短路径了。

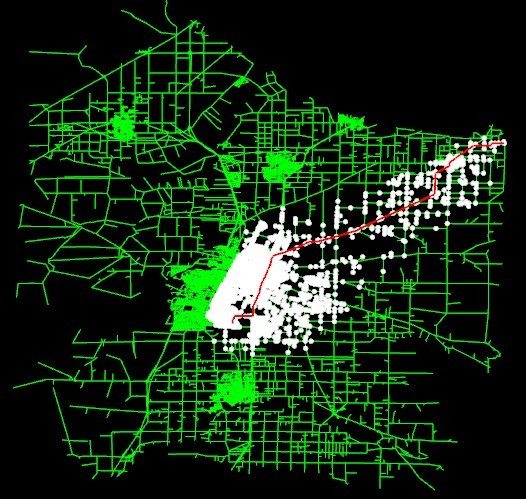
来个例子，下面这是一个城市的公路图网，一共有 18263 个点，23874 条边，视为无向图。我们知道起点和终点的坐标，现在我们要求某两点之间的最短路径。

1. 用 Dijkstra 算法来，其中白色的点表示搜索过程中访问了的点。可以看出 Dijkstra 算法有点像 BFS 向周围扩展，做了很多无用的搜索。当然这与图的形状也有一定关系。

[Dijkstra 访问 18191 个点]

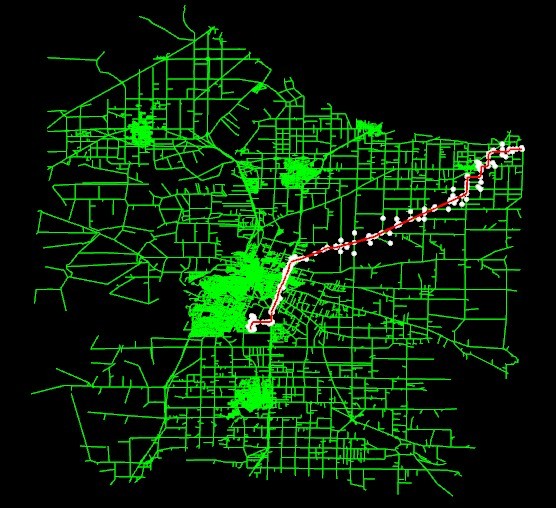
2. 用 A算法，设 S 为起点，T 为终点，启发函数为 F(N)=Path_Dist(S->N)+Dist(N->T)。在搜索过程中 Path_Dist 一直维持着 S->N 的路径长度，Disk(N->T) 的计算可以有多钟选择，这里我选择 Dist(N->T)=sqrt(|Xn-Xt||Xn-Xt|+|Yn-Yt||Yn-Yt|),这个为两点之间的理论最短路径，肯定是满足条件 h(N) <= h(N) 的，那么能得到最优解。可以看到搜索偏向于目标点的方向。

[A* 两点之间距离为评估函数 访问 4398 个点]

3. 另外 (x+y)/2 <= sqrt(x^2+y^2)，所以也可以选择 (|Xn-Xt|+|Yn-Yt|)/2 作为启发函数。但为了节省这个 sqrt 的操作，代价就是访问了更多的点。

[A* (x+y)/2 作为启发函数 访问 14374 个点]

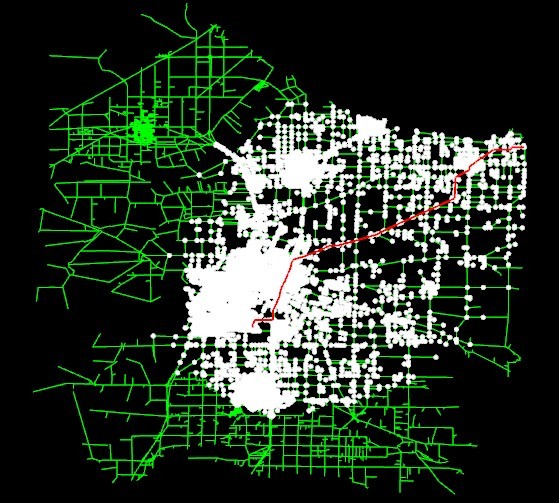
4. 可以做得更好，修改启发函数。Dist(N->T)=|Xn-Xt|+|Yn-Yt|，这为曼哈顿函数，这样就不满足条件 h*(N)<=h(N) 了。所以得不到最优解，但是速度上会快很多，搜索的点也会减少很多。

[A* 曼哈顿距离作为启发函数 访问 296 个点]

大概能得到一个规律，搜索效率依赖于 h(N) 的启发作用，当 h(N) <= h(N) 时候，我们能得到最优解，用第二种启发函数能也满足最优解的条件，但是因为启发用少了所以访问了更多的点。当 h(N)>h(N) 时，得到的可能是比较优的解 (非最短路径)，可以认为因为得到的启发更多 (多到超出了得到最优解的条件限制)，所以能取得更快的效率。这又是一个普遍的问题，在速度、精确度两者之间经常会只能二选一，对于不同的应用从中作出折中。上面那篇论文证明了，对于刚才举例的这个问题，用两点之间的直线距离最为启发函数的 A算法是所有能得到最优解的算法中访问点最少的。启发函数对于特定的问题有特定的取法，那么 A*作为一个搜索的算法框架用处还是挺多的。

Dijkstra＋A* 求 k 短路径

当然这个算法不是我想出来的，这里只是说一下看后自己的理解。在 A算法中，优先队列出来的点如果扩展到了终点，那么 就得到了最短路径。如果能得到实际的评估函数 (也就是 h(N))，那么第二次 从优先队列里面弹出来的就是第 2 段的路径，依次直到 k 短。如何得到 h(N),就是图中各个点到 T 的实际最短路径距离，可以从图的反向图以 T 为源点进行 Dijkstra 算法，最后 Dist[N] 就可以作为 h(N)。然后以 cnt[N] 表示 N 点从优先队列里面弹出来的次数。K-shortest 问题还有更快的解法，不过还没看，这里有大把论文。这里还分结果路径中是否可以有环，像现实中公路网肯定是要求无环的 k-shortest path。下面这个算法是可以有环的。

完整代码如下：

//7040K 282MS
#include <iostream>

#include <queue>
#include <vector>
#include <stdio.h>
#include <cstring>
using namespace std;

const int MAXN=1001;
const int INF=(1<<20);
int N,M; //N 个点 M 条边

int S,T,K; //起点和终点
typedef struct _Edge
{
    int v;//边顶点

    int len;//边长度
}Edge;

int dist[MAXN];
int cnt[MAXN];

bool mark[MAXN];

struct Node{
    int v,len;
    Node() {};
    Node(int a,int b):v(a),len(b) {}
};

bool operator < (const Node& a,const Node& b)
{
    return (a.len+dist[a.v] > b.len+dist[b.v]);
}

vector<Edge> Adj[MAXN];//图的邻接表表示
vector<Edge> Rev[MAXN];//图的逆图

void Init_graph()
{
    int u,v,l;
    Edge edge;
    scanf("%d%d",&N,&M);
    for(int i=0;i<M;i++)
    {
        scanf("%d%d%d",&u,&v,&l);
        edge.v=v;
        edge.len=l;
        Adj[u].push_back(edge);
        edge.v=u;
        Rev[v].push_back(edge);
    }
    scanf("%d%d%d",&S,&T,&K);//计算 S 到 T 的第 K 短路径

    if(S==T) K++;
}

//Dijkstra 算法 找出各个点到 T 的最短距离
void Dijkstra()
{
    memset(mark,false,sizeof(mark));
    for(int i=1;i<=N;i++)
        dist[i]=INF;
    dist[T]=0;
    int u,v,min;
    while(1)
    {
        u=-1,min=INF;
        for(int i=1;i<=N;i++)
            if(!mark[i] && dist[i]<min)
            {
                min=dist[i];
                u=i;
            }
        if(u==-1) break;
        mark[u]=true;
        for(int k=0;k<Rev[u].size();k++)
        {
            v=Rev[u][k].v;
            if(!mark[v] && dist[v]>dist[u]+Rev[u][k].len)
                dist[v]=dist[u]+Rev[u][k].len;
        }
    }
}

int Astar()
{
    if(dist[S]==INF) return -1;
    memset(cnt,0,sizeof(cnt));
    priority_queue<Node> Q;
    Q.push(Node(S,0));
    while(!Q.empty())
    {
        int len=Q.top().len;
        int v=Q.top().v;
        Q.pop();
        cnt[v]++;
        if(cnt[T]==K)
            return len;
        if(cnt[v]>K)
            continue;
        for(int i=0;i<Adj[v].size();i++)
            Q.push(Node(Adj[v][i].v,len+Adj[v][i].len));
    }
    return -1;
}

int main()
{
    Init_graph();
    Dijkstra();
    int ans=Astar();
    printf("%d\n",ans);
    return 0;
}