最近了解到有这么一种数据结构,想拿来在工作中做一些事情,结果效果不好。原来我的理解有一些不对。在这里记录一下。
Crit-bit tree是一种特别的树结构,一般用于存放字符串。Critbit tree 是一种BitWise tries,其树的深度为 O(longest-length),有点像二叉树,不过对于字符串做分支检测的时候代价很小。
Crit-bit 快速高效的支持下面的一些操作:
- 插入一个字符串
- 测试一个字符串是否在树里
- 删除一个字符串
- 查找出树中所有以某个字符串开始的所有字符串
和 hash 有点像,不过 hash 对于第四点没这么方便。
我做了一些性能对比,测试数据是/usr/share/dict/words里面的所有单词,同时做插入和查询的操作。具体测试代码看这里,结果是:
| critbit | 11.6MB | 23.34 |
|---|---|---|
| set | 21.6 MB | 45.85s |
| trie | 332.3 MB | 17.84s |
从中可以看到 trie 树的内存消耗是比较大的,但是查找速度最好。critbit 的内存消耗真的非常小,如果只是把这里所有的单词存下来都要 4MB 的内存,其查找的速度虽然和 trie 树比起来差一些,但还是相当不错。
好好的研读了 crit-bit 的实现和这篇文章,里面技巧挺多的。 critbit 的结构很简单:
typedef struct{
void* child[2];
uint32 byte;
uint8 otherbits;
}critbit0_node;
typedef struct{
void* root;
}critbit0_tree;
其中 child 是 void*指针,对于树的内部节点其指向的是子节点,对于叶子节点其指向的是字符串。 byte 用来表示当前节点匹配的长度,otherbits 是一个 mask,可以用来快速的取得不同最高位,在查询的过程中用这个来做 branch。
具体的代码分析这里比较少,最复杂的函数是 critbit0_insert。在插入过程中需要记录下来 byte 和 otherbits,
并且更新前面的父节点。
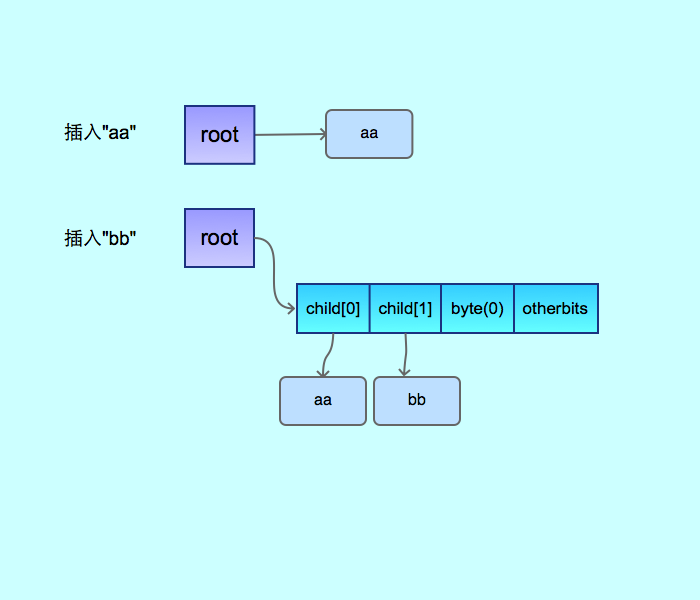
然后再继续插入后的结构变化是:
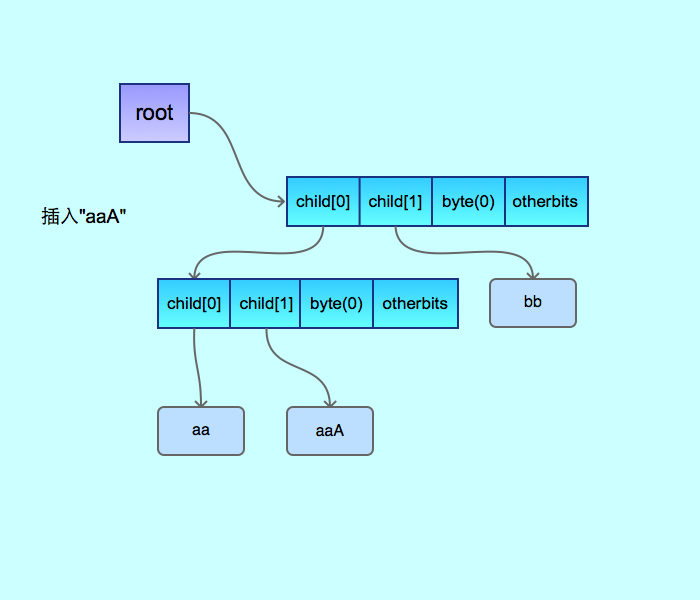
下面记录一下其中的几个技巧。
align 指针最后一位用来做标志
树的结构需要一个标志变量来表示是否是内部节点或者是叶子节点。这个变量如何能省掉? 看上面的 void* root 和 void* child,都是即可以用来指向字符串又可以指向节点,一般申请过来的指针变量都是 align 好的,所以最低位为 0,这是可以拿来用的。因此对于内部节点我们可以在这个位上设置为 1,只是要注意在通过这个指针取值的时候需要减回去。
a = (posix_memalign((void**)&x, sizeof(void*), ulen+1))
posix_memalign 在这里用的是 sizeof(void*),其实就和 malloc 一样了,因为一般 Linux 上编译器和 C 库已经处理了对齐问题。
因此在查找的这段代码里是这样的:
int critbit0_contains(critbit0_tree*t, const char* u) {
const uint8* ubytes= (void*)u;
const size_t ulen= strlen(u);
uint8* p= t->root;
if(!p) return 0;
while( 1 & (intptr_t)p ){ //内部节点?
critbit0_node* q = (void*)(p-1); //取得真正的指针
uint8 c = 0;
if(q->byte < ulen) c = ubytes[q->byte];
const int direction= (1+(q->otherbits|c))>>8;
p = q->child[direction];
}
//叶子节点
return 0 == strcmp(u, (const char*)p);
}
取最高位的非 0bit
在插入过程中计算最高位的不同位。
newotherbits = p[newbyte]^ubytes[newbyte];
其实也可以用一个 for 循环来计算,不过这里是这样实现的:
newotherbits |= newotherbits>>1;
newotherbits |= newotherbits>>2;
newotherbits |= newotherbits>>4;
这相当于是计算不小于它的 2 的整数次幂,对于 32bit 的代码可以看看这里的next_pow_of_2。
文章和代码,其中那篇文章有详细分析。

