从椭圆曲线到 secp256k

区块链这行经常会和椭圆曲线密码算法打交道，我也在尝试理解这其中的数学原理，这里记录一下。

什么是椭圆曲线 (elliptic curve)

先想象一个普通的曲线，比如抛物线（抛个球的轨迹）。椭圆曲线不是椭圆（名字有点误导），而是一种长得像“对称小山丘”或者“歪歪扭扭的环”的数学图形。

椭圆曲线通常表示为：

$$ y^2 = x^3 + ax + b$$

通过这个方程我们可以看到椭圆曲线是上下对称的，其中 (a) 和 (b) 是曲线参数，比如下面这些曲线就是 b = 1 的情况下，a 从 2 变到 -3 的情况：

我们通常使用的椭圆曲线必须满足非奇异 的特征，这些参数必须满足判别式：

$$4a^3 + 27b^2 \neq 0$$

“非奇异”什么意思？在数学上，椭圆曲线要是“非奇异”（non-singular），就是说这条曲线长得“光滑正常”，没有奇怪的尖角、交叉点或者自己打结的地方。简单讲，就是曲线不能太“怪”，得是个平滑的、像个正常曲线的样子。

如果曲线“奇异”了，会出现两种毛病：

尖点（Cusp）：曲线像被捏了个尖角，某个地方变成一个尖尖的点，不光滑了。
自交点（Node）：曲线自己交叉，像个“X”形，两个方向撞一块儿了。

这些毛病会让“点加法”出问题，因为公式会算不下去，或者结果不唯一。关于点加法我们后面再谈，下面这两个椭圆曲线都是奇异的：

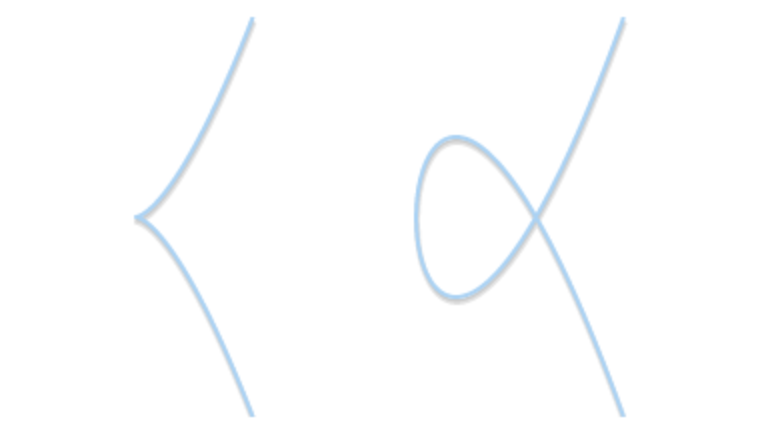
阿贝尔群 (Abelian group)

这名字来自数学家 Niels Henrik Abel，他研究了这种“顺序无所谓”的结构。

“群”（group）是数学里的一种概念，就像一个有规则的“俱乐部”。里面有一堆东西（叫元素），加上一个玩法（叫运算），得满足几个条件。阿贝尔群是群的一种特别类型，特点是这个玩法“顺序无所谓”。
简单说，阿贝尔群就是一个集合，里面有些元素，能用某种运算（比如加法）组合起来，满足以下条件，而且运算顺序随便换都没问题。

群的四个基本条件：

能玩（封闭性）：你拿集合里两个东西玩一下（做运算），结果还是集合里的东西。比如，两个整数相加还是整数。
有老大（单位元）：集合里有个特殊的东西，跟谁玩都不变。比如加法里的 0，$0+5=5$ ，什么也没变。
能回头（逆元）：每个东西都有个“反着玩”的朋友，俩人玩一下变老大。比如加法里，5 的逆元是 −5，$-5 + 5 = 0$。
括号随便（结合律）：玩的时候，先跟谁玩再跟谁玩都一样。比如 (2+3)+4=2+(3+4) 。

群变成“阿贝尔群”，还得多一条：

顺序无所谓（交换律）：你拿两个东西玩，先后顺序换一下，结果一样。比如 $2+3 = 3+2$，都是 5。如果顺序有所谓（比如 $2−3≠3−2$），那就不是阿贝尔群了。

密码学里用阿贝尔群（像椭圆曲线），因为它简单又有规律，适合搞安全。

椭圆曲线上的离散点

到了 1900 年代，椭圆曲线跟数论彻底绑定，而数论研究的是整数。

椭圆曲线方程

$$y^2 = x^3 + ax + b$$

通常是在普通实数（无限多的小数）上定义的，画出来是个连续的曲线。但安全领域说的椭圆曲线通常是说通过椭圆曲线定义出来的群，其范围定义在某个有限域 : $F_p$ 。

简单说，整数也是一个无限数字的世界，而有限域就是一个只有有限个数字的“数字世界”。这里的表示这个世界里只有 0, 1, 2, ..., p-1 这 (p) 个数，(p) 必须是个素数。为什么是素数？因为这样能保证这个小世界里的数学运算（加减乘除）不会出乱子，规则特别“干净”。

在这个有限域里，所有的计算结果都得落在这 (p) 个数里面。如果算出来超了 (p)，就“绕回去”，用模 (p) 的方式把结果限制住。比如在 $F_5$ 里：3+4=7，但 7 不在范围内，所以 $7mod 5=2$，所以结果是 2。

这个时候，曲线不再是连续的，而是变成了散落在 $F_p \times F_p$ 网格上的一堆离散的点。比如我这个程序打印出来这条曲线上的点，这里打印的时候 $y =0$ 是在中间，从中间看上下是对称的：

点加法和对数问题

上面我们只是通过椭圆曲线找到了一组数字，但这些数字之间还需要一种操作，这种操作才能让这些离散的数字组成一个群的概念。这里就需要引入一个“点加法”的概念。

点加法就像一个魔法公式，告诉你怎么从一个点“跳”到另一个点，或者同一个点“跳”两次变成新点。想象椭圆曲线是一条弯弯曲曲的线，上面有很多点，在不断做点加法的过程中不断地移动点。

在椭圆曲线上，点加法有几何和代数两种解释：

几何解释：通过两个点画一条直线，与曲线的第三个交点取关于 x 轴的对称点。
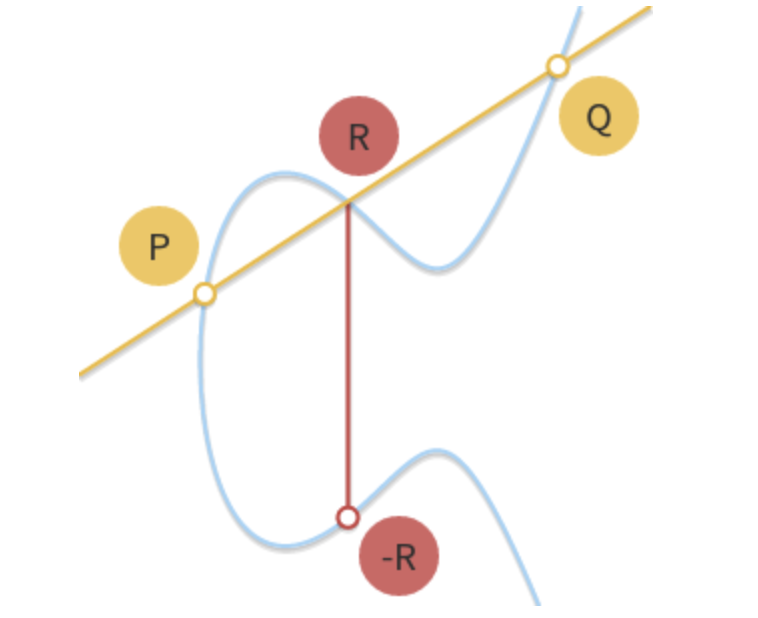
代数公式：

离散对数问题是在一个有限的“数字圈”里玩，比如有限域 $F_p$ （( p ) 是素数）或者椭圆曲线的点群里。比如：

给你 $y = g^x \mod p$ ，已知 ( y, g, p )，求 x。
在椭圆曲线上，变成 $Q = k \cdot P$ ，已知 Q 和 P（基点），求 k（跳了几次）。

这里的 ( x ) 或 ( k ) 就是“离散对数”。这就是离散对数问题，数学家没找到一个快速方式能解决这个问题。

直观感受一下，我们修改上面那个程序，我定义一个起始点 P，然后不断通过 P + P 的方式进行 20 次，终点是黄色的，然后把中间通过的点用蓝色的线连接起来，可以看到我们经过的点是没有什么规律的。

反向破解就比如你拿到这幅图，如果不告诉你蓝色的连线，而只有那个黄色的终点，现在问你起点在哪里？这个问题是很难回答的。

19 世纪数学家就研究过椭圆曲线的性质，但到 20 世纪数学家发现椭圆曲线上的点能通过点加法这类操作组成一个阿贝尔群，这些点的数量和分布特别“诡异”——既有限，又乱得没规律。而点加法这种正向容易、逆向难的特征刚好就适用于密码学。

从椭圆曲线到密码学

Neal Koblitz 是专攻数论的数学家，对椭圆曲线很熟。他当时在研究有限域上的数学问题，注意到椭圆曲线的点群和传统离散对数有点像，但更“紧凑”。他想：如果把 Diffie-Hellman 的思路搬到椭圆曲线上，会不会更高效。

Victor Miller 在 IBM 搞应用数学，也盯着椭圆曲线的群性质。他发现，椭圆曲线的离散对数问题（ECDLP）似乎比普通离散对数还难破解，而且需要的数字（密钥长度）小得多。他俩不谋而合，都觉得这玩意儿能干大事。

他们的想法不是凭空来的，有几个关键“火花”：

群论的启发：密码学里的 Diffie-Hellman 用的是乘法群，Koblitz 和 Miller 看到椭圆曲线的点群也是阿贝尔群，觉得可以“照搬”过来。
Hasse 定理：20 世纪数学家 Hasse 证明了椭圆曲线在 $F_p$ 上的点数大概是 $p + 1 \pm 2\sqrt{p}$，数量够大但分布随机，正好适合做离散对数问题。
效率优势：他们算了算，椭圆曲线的运算（点加法和倍点）虽然复杂，但用小得多的数字（比如 160 位）就能达到传统方法 1000 位的安全级别，这对硬件来说太诱人了。

为什么不随便挑个别的曲线？因为椭圆曲线（三次方程）正好有“三个交点”的几何性质，点加法规则简单又优雅，其他高次曲线要么太复杂，要么安全性不够。加上数学家几百年的研究，椭圆曲线的性质已经摸得透透的，拿来用最保险。

椭圆曲线加密从 1985 年的“怪胎”到今天的核心技术，走过了从冷门到爆款的路。它的历史是个典型的“学术变实用”的故事：数学家玩了好多年的椭圆曲线，被 Koblitz 和 Miller 一挖掘成了安全的利器。

secp256k1

secp256k1 是一个特殊的椭圆曲线，名字听起来高大上，其实就是密码学里用的一条数学曲线，secp256k1 的名字可以分成几个部分：

sec：Standards for Efficient Cryptography（高效加密标准）。
p：Prime（素数），表示这个曲线是用素数域定义的。
256：表示这个曲线的“大小”是 256 位（也就是密钥长度）。
k：Koblitz 的缩写，指的是数学家 Neal Koblitz，他研究了这种类型的曲线。
1：表示这是 Koblitz 曲线中的第一个（最简单的一个）。

它是比特币、以太坊这些区块链的“安全锁”的核心。简单说，它定义了一个“跳跃游戏”的规则，靠这个规则保护你的私钥和公钥。

secp256k1 是这么来的：

方程：它的公式是 $y^2 = x^3 + 7$ 注意，这里的 $a = 0 , b = 7$，是个很简单的椭圆曲线。
有限域：它不是在普通数字上玩，而是在一个超级大的“数字圈” $F_p$ ，这里的 (p) 是个特定的素数，大约是 $2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1$。
基点 (P)：它有个固定的起跑点 (P)，坐标是 $(x_P, y_P)$，具体值很长（见下面），但它是公开的，大家都从这点开始跳。

secp256k1 就像一个超级复杂的“跳格子游戏”：

你挑一个秘密数字 (k)（私钥），从基点 (P) 开始，用点加法跳 (k) 次，跳到的点是 $Q = k \cdot P$
公钥。
别人看到 (P) 和 (Q)，想猜你跳了几次 (k)，但因为点加法逆运算（离散对数问题）太难，他们算不出来。

类比一下，想象 secp256k1 是个巨大的迷宫，里面有 (p) 个格子（大概 $2^{256}$个，这个数字大到超乎想象，比宇宙里的原子、沙粒、甚至时间秒数都多得多。它不是“很大”，而是“大的离谱”）。迷宫的形状由上面的椭圆曲线决定，起点是 (P)。你拿着私钥 (k)，按迷宫的跳法（点加法）走 (k) 步，停在 (Q)。这个迷宫设计得太巧妙，别人站在 (Q) 看你走过的路，根本摸不着头脑，只能从 (P) 一步步试，试到宇宙爆炸也试不完，破解难度像“从银河系找一粒沙”。签名时，拿私钥和消息算出两个数（r, s），别人用公钥验证。

secp256k1 另外一个特点是计算快，主要来自它的特殊数学结构和参数选择。bitcoin-core/secp256k1 是高度优化过的 C 语言实现，用了预存表、内敛汇编等各种优化手段来提高效率。通常我们在 Rust 程序上用的也是这个库的 binding。