一个有趣的问题，据说这个题目耗费了 Don Knuth 24 小时解决。一起来看看。

You are given an array of integers of length n, where each element ranges
from 0 to n - 2, inclusive. Prove that at least one duplicate element must
exist, and give an O(n)-time, O(1)-space algorithm for finding some
duplicated element. You must not modify the array elements during this
process.

这有几个重要的约束，O(n)，O(1) 的复杂度，不能修改这个数组。可能有多个数重复了，但至少有一个数重复了。

首先第一个证明问题，等价于 n 个鸽子，n-1 个笼子，那么至少有一个笼子里面有 2 个鸽子，就是鸽笼原理 (抽屉原理), 反证法可以证明。

难的是第二个问题，假设 a[0, n], 值都在 0,1, …, n-2 范围内。如果扫描这个数组，重复的会出现第二次 (废话，囧)，
关键是只能用 O(1) 的空间，否则用空间记录出现过的就行了。如果把数组看成一个映射，i -> f(i) = a[i]，那么这个问题可以转换成更抽象的模型。举个例子：

n = 6
index: 0 1 2 3 4 5
value: 1 4 0 0 3 2

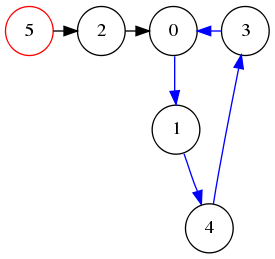
其 index 对应 value 映射为为 0->1, 1->4, 2->0 等等，那么把这个图画出来就是这样：

这个问题转换为求图中环开始的点，因为出现环说明某个点重复出现了。从 5 开始遍历这个图会在 0 处发现环，为什么选取 5，因为 5 肯定为一个起点，并且不在 0~N-2 内。其实只要选取不孤立的那个点当作起点就可以检测环，极端情况比如：

n = 6
index: 0 1 2 3 4 5
value: 0 1 2 4 5 3

选择 index=5 还是可以发现环，如果选取 0 就发现不了 3 和 4,5 之间的那个环。

[Cycle detection] 是一个经典的计算机问题。经典的算法是 Floyd’s cycle-finding algorithm，这个算法简单而优美。严格的数学证明当然可以，也能更明显的从现实经验得出结论。如果一个赛道中间出现某个环 (分两种情况，赛道本身是环、赛道前面有一段没环而中间出现一个环 9 字形)，求这个环的周长 C。让两位运动员同时出发，并且 P1 的速度是 P2 的两倍，当他们第一重新相遇的时候，一定是在环的某个点上，并且其路程之差为这个环的周长的 K 倍 (K>=1)，这解决了一部分问题，我们知道了 KC 的值，如果 K==1，则得出结果，说明两人刚好是在环开始点相遇。否则就是在环内其余点相遇，可以得知现在 P2 的路程为 KC(P1 的路程为 2KC), 如果让 P3 以和 P2 同样的速度从起点开始，P2 继续从相遇点开始跑，那么 P2 和 P3 肯定还会相遇，并且相遇的点一定为环开始点！回到这个问题，这个 index 的值就是重复的值。代码描述如下：

int detectCycle(int* seq， int Num)
{
    int slow = Num -1;
    int fast = Num -1;
    while(1) {
        slow = seq[slow];
        fast = seq[seq[fast]];
        if(slow == fast)
            break;
    }
    int finder = Num - 1;
    while(1) {
        slow = seq[slow];
        finder = seq[finder];
        if(slow == finder)
            break;
    }
    return finder;
}

算法描述很简单，但其中思维的却很有乐趣。以前同样有一个问题，检测一个链表是否有环，这是由此出来的一个特例，因为对于一个链表的每个节点除了头节点都有一个前节点和后节点 (无环则末节点指向空)，而图是一个更通用的模型。

bool hasCycle(ListNode *head) {
  ListNode* slow = head;
  ListNode* fast = head;
  while(fast && fast->next) {
      slow = slow->next;
      fast = fast->next->next;
      if(slow == fast)
        return true;
    }
  return false;
}