编程珠玑里面代码优化这一章。

问题 1 函数，宏，内联代码

#define max(a,b) ((a)>(b)? (a):(b))

float max(float a,float b)
{
    return a>b? a:b;
}
inline float max(float a,float b)
{
    return a>b? a:b;
}

上面这个函数到底哪一个快一些？测试了一下。宏效率是高一点，但是对于加上编译器优化以后基本没什么区别了。

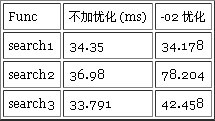
问题 2 顺寻搜索

int search1(int v)
{
    for(int i=0;i<N;i++)
        if(vec[i]==v)
            return i;
    return -1;
}

int search2(int v)
{
    vec[N]=v;
    int i;
    for(i=0; ;i++)
        if(vec[i] == v)
            break;
    if(i==N)
        return -1;
    return i;
}


int search3(int v)
{
    vec[N]=v;
    int i;
    for(i=0; ;i+=8)
    {
        if(vec[i]==v) break;
        if(vec[i+1]==v) {i+=1; break;}
        if(vec[i+2]==v) {i+=2; break;}
        if(vec[i+3]==v) {i+=3; break;}
        if(vec[i+4]==v) {i+=4; break;}
        if(vec[i+5]==v) {i+=5; break;}
        if(vec[i+6]==v) {i+=6; break;}
        if(vec[i+7]==v) {i+=7; break;}
    }
    if(i==N)
        return -1;
    return i;
}

这三个函数哪一个效率最好？据说第二个提高 5%，第三个会提高 10%~20%(对于老实计算机)。在我的机子上测试了一下，N=10000000。并不如书上说的能提高多少，反而最原始的写法在优化后效率更高，确实是这样的数据。

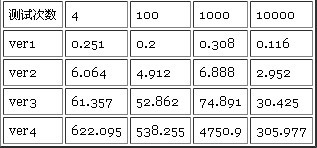
问题三 二分查找

数组大小为 1000。单位 ms。

确实第二个版本提高了一些，第四个版本甚至提高了一半的效率。

测试是一个麻烦的事情，因为同一时间处理器调度了其他进程，但多次测试还是能给一个大概的印象。第二个例子的优化没起什么作用，也许现在的编译器优 化技术比以前更好的，得出的结果并不如书上所说。在一个算法复杂度确定的情况下改变一些写法会有一点提升，但是对于不同的输入规模也许就得不到什么提高，而且编译器优化以后基本差别就更小了。为了那么一点效率的 提升增加了代码的复杂度得不偿失。原理那章也说了，不成熟的优化是大量编程的祸害，会危机程序的正确性、功能性、和可维护性。王道还是改变数据结构或者算法，除非确定一个部分的代码会经常被调用很多次，在这里可以花一些功夫去优化。优化是把双刃剑，玩火者，小心自焚，哈哈。