dicker

随机数代表着不确定性，其在计算机中广泛使用，比如用作加密的 key、密码的生成、模拟，扑克游戏中，还有一些经典的算法 (比如Monte Carlo) 依赖随机数的产生。以下是一些随机数相关的问题简单总结。

随机数产生，真随机数和伪随机数生成器

随机数的产生是一个很有趣的问题。我们希望只通过计算机来产生随机数的时候会有一些困难，计算机擅长做确定的事情，按照制定的指令去依次执行。
有两种产生随机数的方法，真随机数和伪随机数，这两种有各自的优点和缺点。

伪随机数生成器 (PRNG)，顾名思义产生的不是严格意义上的随机数，一般是通过一些数学公式 (或者计算好的表) 来产生。比如简单的Linear congruential generator，可以用来产生伪随机数。伪随机数的行为是可被预测的，但是在统计意义上来说是随机的。因为这个特点其所以使用范围有限，比如一些模拟程序。而且伪随机数有可能出现固定的周期，比如下面这两幅图分别是通过真正的随机数产生器和 Windows 下面的 PHP 的伪随机数生成器产生的 Bitmap，可以清楚地看到右边的那副图有规律可循。

另外如 Borland 随机数生成器 Random 的实现：

long long RandSeed = #### ;
unsigned long Random(long max)
{
    long long x ;
    double i ;
    unsigned long final ;
    x = 0xffffffff;
    x += 1 ;

    RandSeed *= ((long long)134775813);
    RandSeed += 1 ;
    RandSeed = RandSeed % x ;
    i = ((double)RandSeed) / (double)0xffffffff ;
    final = (long) (max * i) ;

    return (unsigned long)final;
}

真随机数生成器 (RNG)，通过向计算机中引入一些不可预测的物理信息，比如键盘敲击和鼠标移动等。所以真随机数才是很难预测的或者根本来说不可预测。每个操作系统的实现有各自的区别，
比如 Linux 中产生随机数引入了物理噪音作为输入，比如 mac 地址可以用来初始化 entropy pool，随机源可以加入中断时间，硬盘的寻址时间等等。
接口是/dev/random、/dev/urandom、get_random_bytes()，其中 get_random_bytes 在内核中使用。
/dev/random 和/dev/urandom 的区别是/dev/random 强度更大并且是阻塞的，因为要收集更多熵。

随机数的使用

涉及到随机数的程序要特别小心。比如一个很简单的程序，我们知道 C 语言中的 rand() 产生的随机数是有范围的，0～32767，如果我要生成范围在 0～10 的随机数如何做？
可能你会简单认为 rand()%10 可以得到 (惭愧我以前也这样用的)，但是这真的是随机的吗？如果你把 0～32767 的所有数字依次%10，统计一下可以发现有的数出现的次数要大一些，因此最后出现某些数的概率相应的要大一些。

另外一个思考题，给一个 rand() 可以产生 [1, 5] 之间的随机整数，利用这个 rand 产生 [1, 7] 之间的随机整数？

另写一个抽奖程序，从 30w 个用户中随机抽取 10w 个中奖用户？

写个好的洗牌程序不容易

dicker

写一个对的洗牌程序看起来很容易，其实不然。Robert Sedgewick 说过：

That’s a pretty tough thing to have happen if you’re implementing online poker.You might want to make sure that if you’re advertising that you’re doing a random shuffle that you go ahead and do so.”

—Robert Sedgewick, Professor of Computer Science, Princeton

比如 ASF Software 在多年前写的一个流行的网上扑克游戏，其中的洗牌程序是这段 Pascal 代码：

procedure TDeck.Shuffle;
var
   ctr: Byte;
   tmp: Byte;
   random_number: Byte;
begin
   { Fill the deck with unique cards }
   for ctr := 1 to 52 do
      Card[ctr] := ctr;
   { Generate a new seed based on the system clock }
   randomize;
   { Randomly rearrange each card }
   for ctr := 1 to 52 do begin
      random_number := random(51)+1;
      tmp := card[random_number];
      card[random_number] := card[ctr];
      card[ctr] := tmp;
   end;
   CurrentCard := 1;
   JustShuffled := True;
end;

可以分析一下这里的好几处问题，这里的洗牌算法也有问题，52！个排列出现的概率不一样。拿三张牌来作为例子就明白了。

for (i is 1 to N)
    Swap i with random position between 1 and N

dicker
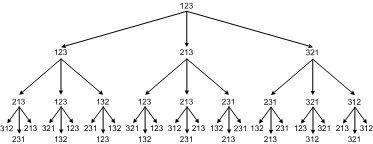可以看出 231, 213, 132 出现的次数要多一些，因此相对应的概率也大。

正确的洗牌程序算法是：

for (i is 1 to N)
    Swap i with random position between i+1 and N

一个 32 位的数作为 seed，对于伪随机长生器是有问题的，因为如果给定 seed 伪随机产生器的行为是可以预测的。
32 的 seed 的所有可能值的个数为 2^32 个，这相比 52!(8.0658 * 10 ^ 67) 小得很多。所以对于 32 位的 seed，甚至可以用蛮力法来攻破。

其他

摘自<<思考的乐趣>>10 个人坐在一起谈天，突然他们想知道他们的平均年薪是多少，但每个人都不愿意透露自己的工资数额，有没有什么办法让他们能够得到答案，并不用担心自己的年薪被曝光？
一个简单的协议模型，当然与随机数有点关系。

参考：

Wiki: Random number generation。

How We Learned to Cheat at Online Poker: A Study in Software Security。

顾森，思考的乐趣。