正则表达式匹配是一个经典问题，这里有一个问题。
实现 isMatch，其中。表示任意一个字符，*表示 0 个或者任一个前面的字符：

isMatch("aa","a")       → false
isMatch("aa","aa")      → true
isMatch("aaa","aa")     → false
isMatch("aa", "a*")     → true
isMatch("aa", ".*")     → true
isMatch("ab", ".*")     → true
isMatch("aab", "c*a*b") → true

这是一个正则表达式问题的简化版本只有.和*，可以用递归来解决。正则表达式涉及到自动机理论，顺便再复习一下当年没好好学的东西。查找一番后发现了这篇 Russ Cox 写的文章非常好 (这家伙写了不少文章，xv6 里也有他的代码，现在在为 Go 项目工作)。于是我也尝试着用 DFA 来解决这个问题。

DFA 和 NFA 的概念

首先对于没一个正则表达式都有一个对应的 DFA 可以来表示，DFA 是 Deterministic Finite Automaton 的简称，还有 NFA(Non-deterministic Finite Automata)。NFA 对于一个字符的输入有可能存在多个以上的状态转移，而 DFA 对于没一个输入只存在一个选择。所以每一个 NFA 都可以转化为一个 DFA，但是一个 DFA 可以转化为多个 NFA。我们来看一个例子：

对于正则表达(a|b)*abb的 NFA 和 DFA 分别表示为：

nfa

dfa

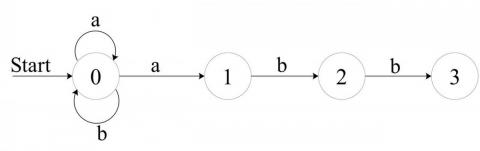
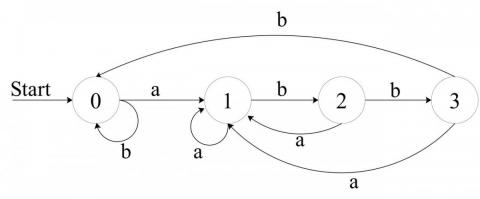
DFA 的状态数目和 NFA 一样，但是一般实践过程中 DFA 的状态转移要多，所以 DFA 相对来说要难构造一些，同时 DFA 比 NFA 需要的内存空间更大。正因为在 NFA 中一个状态可能向多个状态转移，在极端的情况下其效率比不过 DFA。更多关于正则分类可以参考正则表达式引擎及其分类。

对于 NFA 不同的实现效率会不一样，这也是 Russ 的文章里所说的。Russ 的文章里面介绍了 Thompson NFA 算法实现 (没错就是发明 C 的那神)，一些老的 Unix 工具是用的这个算法，比如 Awk，Tcl，GNU grep 等，而一些更通用的编程语言用的是基于回溯的一种 NFA 实现，比如 Perl/Python。通过数据比较，在最坏的情况下用 Thompson NFA 实现的 awk 表现比匹配回溯的 NFA 要好很多倍。最坏情况下的复杂度不一样，回溯 NFA 是 O(2^N)，而 Thompson 的复杂度是 O(N^2)。文中的代码可以号好看看，非常简洁的 C 实现。

一个尝试实现

对上面那个问题我尝试着实现了一个程序构建 DFA 来解决，提交上去完成 439 个测试用例只用了 28ms，相对于递归版本的需要 104ms。也可能 LeetCode 上面的测试数据太少，比较的意义不大。代码长度当然要比递归的长不少。
定义 State：

enum OpType {
    ZERO_PLUS_ONE,
    ANY_ONE,
    MUST_ONE
};
struct State {
    OpType         type;
    int            id;
    char           value;
    bool           end;
    State*         prev;
    vector<State*> next;

    State(OpType t, int i, char v, State *p) :
        type(t), id(i), value(v), end(false), prev(p) {
        if(type == ZERO_PLUS_ONE)
            next.push_back(this); 
        if(p == NULL)
            prev = this;
    }

    void add(State* n) {
        next.push_back(n);
        // 匹配任意，前驱加上当前需要添加的状态
        if(type == ZERO_PLUS_ONE && prev != NULL) 
            prev->add(n);
    }
};

构建 DFA 的过程如下，注释的部分需要注意：

State* construct_dfa(const char* pattern) {
    if(pattern == NULL) return NULL;
    const char* p = pattern;
    State* start = new State(ANY_ONE, Num, '.', NULL);
    State* cur   = start;
    State* next  = NULL;
    char   prev  = '.';
    Num = 1;
    while(*p && *p != '\0') {
        if(*(p+1) != '*') {
            OpType type;
            char value;
            if(*p == '*') {
                type = ZERO_PLUS_ONE; //匹配 0 个或者多个
                value = prev;
            } else {
                value = *p;
                type = *p == '.'? ANY_ONE : MUST_ONE; //匹配任意一个。或者指定的字符
            }
            next = new State(type, Num, value, cur);
            prev = *p, p++;
        } else {
            next = new State(ZERO_PLUS_ONE, Num, *p, cur);
            prev = '*', p+=2;
        }
        cur->add(next);
        cur = next;
        Num++;
    }
    cur->end = true;
    // 例如  ab*a*c*  对于 "a"，即使后面几个*, "a"也算是一个 end，
    while(cur->type == ZERO_PLUS_ONE) {
        cur = cur->prev;
        cur->end = true;
    }
    return start;
}

匹配的过程就是一个搜索的过程，需要注意避免重复访问，另外如果下一层要访问的为空就可以退出整个搜索过程了，整个代码看这个Gist。